排序算法05：归并排序

2017-04-29

算法介绍

归并排序的算法逻辑为把两个有序的数组归并为一个有序的数组。

举个例子，对于一个长度为8的数组，有两种归并方式

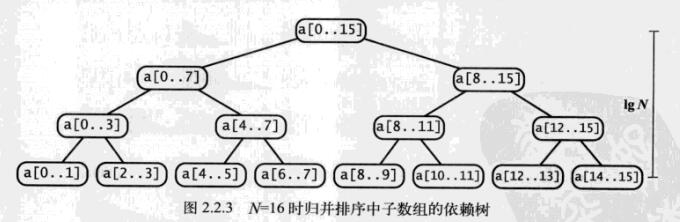
自顶向下的归并:

先分为[0-3],[4-7],左右有序后再归并到一起就变成一个完整的有序数组了
让[0-3]有序又可以分为[0-1]、[2-3]有序，递归下去，最终归并为[0-3]有序

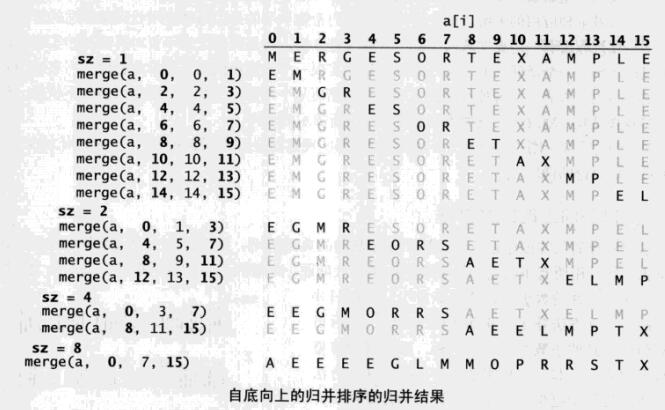
自底向上的归并：

先让[0-1],[2-3],[4-5],[6-7]有序
再让[0-3],[4-7]有序
最终归并[0-7],让整个数组有序

归并实现

/**
 * 原地归并
 * @param arr
 * @param start
 * @param mid
 * @param end
 */
function merge(arr,start,mid,end) {
    var i=start,j=mid+1;
    var temp = [];
    //数据复制一份将a[start..end]复制到temp[start..end],start不一定为0
    for(var m=start;m<=end;m++){
        temp[m] = arr[m];
    }

    for(var n=start;n<=end;n++){
        if(i>mid){
            //左边用尽（取右半边的元素）
            arr[n] = temp[j++];
        }else if(j>end){
            //右边用尽（取左半边的元素）
            arr[n] = temp[i++];
        }else if(temp[j]<temp[i]){
            //右半边的元素小于左半边的元素（取右半边的元素）
            arr[n] = temp[j++];
        }else{
            //右半边的元素大于左半边的元素（取左半边的元素）
            arr[n] = temp[i++];
        }
    }
}

下面这张原地归并轨迹的样例图来自于《算法》第四版，左侧为arr，右侧为temp数组

自顶向下的归并

/**
 * 自顶向下的归并
 * @param arr
 * @param start
 * @param end
 */
function sortDown(arr,start,end) {
    //将数组arr[start..end]排序，这里的start并不一定是0
    if(end<=start) return;
    var mid = start + parseInt((end-start)/2);
    sortDown(arr,start,mid);        //- 将左半边排序
    sortDown(arr,mid+1,end);        //- 将右半边排序
    merge(arr,start,mid,end);       //- 归并结果
}

自底向上的归并

/**
 * 自底向上的归并
 * @param arr
 */
function sortUp(arr) {
    var len = arr.length;
    for(var sz=1;sz<len;sz=2*sz){
        for(var start=0;start<len-sz;start=start+2*sz){
            merge(arr,start,start+sz-1,Math.min(start+2*sz-1,len-1));
        }
    }
}

完整代码

javascript实现

/**
 * Created by YiYing on 2017/4/29.
 */

/**
 * 原地归并
 * @param arr
 * @param start
 * @param mid
 * @param end
 */
function merge(arr,start,mid,end) {
    var i=start,j=mid+1;
    var temp = [];
    //数据复制一份将a[start..end]复制到temp[start..end],start不一定为0
    for(var m=start;m<=end;m++){
        temp[m] = arr[m];
    }

    for(var n=start;n<=end;n++){
        if(i>mid){
            //左边用尽（取右半边的元素）
            arr[n] = temp[j++];
        }else if(j>end){
            //右边用尽（取左半边的元素）
            arr[n] = temp[i++];
        }else if(temp[j]<temp[i]){
            //右半边的元素小于左半边的元素（取右半边的元素）
            arr[n] = temp[j++];
        }else{
            //右半边的元素大于左半边的元素（取左半边的元素）
            arr[n] = temp[i++];
        }
    }
}

/**
 * 自顶向下的归并
 * @param arr
 * @param start
 * @param end
 */
function sortDown(arr,start,end) {
    //将数组arr[start..end]排序，这里的start并不一定是0
    if(end<=start) return;
    var mid = start + parseInt((end-start)/2);
    sortDown(arr,start,mid);        //- 将左半边排序
    sortDown(arr,mid+1,end);        //- 将右半边排序
    merge(arr,start,mid,end);       //- 归并结果
}

/**
 * 自底向上的归并
 * @param arr
 */
function sortUp(arr) {
    var len = arr.length;
    for(var sz=1;sz<len;sz=2*sz){
        for(var start=0;start<len-sz;start=start+2*sz){
            merge(arr,start,start+sz-1,Math.min(start+2*sz-1,len-1));
        }
    }
}

//测试代码
(function () {
    var arr1 = [4,5,6,0,3,5,21,7,9,0,1];
    console.log(arr1);
    sortDown(arr1,0,arr1.length-1);
    console.log(arr1);
    console.log("----------------");
    var arr2 = [4,5,6,0,3,5,21,7,9,0,1];
    console.log(arr2);
    sortUp(arr2);
    console.log(arr2);
})();

java实现

package com.algs;

public class Merge {

	private static void merge(int[] arr,int[] temp,int start,int mid,int end){
		int i=start,j=mid+1;
		//避免每次都创建数组对象
		//int[] temp = new int[arr.length];
		//数据复制一份将a[start..end]复制到temp[start..end],start不一定为0
		for(int m=start;m<=end;m++){
			temp[m] = arr[m];
		}
		for(int n=start;n<=end;n++){
	        if(i>mid){
	            //左边用尽（取右半边的元素）
	            arr[n] = temp[j++];
	        }else if(j>end){
	            //右边用尽（取左半边的元素）
	            arr[n] = temp[i++];
	        }else if(temp[j]<temp[i]){
	            //右半边的元素小于左半边的元素（取右半边的元素）
	            arr[n] = temp[j++];
	        }else{
	            //右半边的元素大于左半边的元素（取左半边的元素）
	            arr[n] = temp[i++];
	        }
	    }
	}

	private static void sortDown(int[] arr,int[] temp,int start,int end){
		//将数组arr[start..end]排序，这里的start并不一定是0
	    if(end<=start) return;
	    int mid = start + (end-start)/2;
	    sortDown(arr,temp,start,mid);        //- 将左半边排序
	    sortDown(arr,temp,mid+1,end);        //- 将右半边排序
	    merge(arr,temp,start,mid,end);       //- 归并结果
	}

	private static void sortUp(int[] arr,int[] temp){
		int len = arr.length;
	    for(int sz=1;sz<len;sz=2*sz){
	        for(int start=0;start<len-sz;start=start+2*sz){
	            merge(arr,temp,start,start+sz-1,Math.min(start+2*sz-1,len-1));
	        }
	    }
	}

	public static void main(String[] args) {
		int[] arr1  = {4,5,6,0,3,5,21,7,9,0,1};
		int[] temp1 = new int[arr1.length];
	    sortDown(arr1,temp1,0,arr1.length-1);
	    for(int m:arr1){
	    	System.out.print(m+" ");
	    }

	    System.out.println();
	    System.out.println("----------------");

	    int[] arr2  = {4,5,6,0,3,5,21,7,9,0,1};
	    int[] temp2 = new int[arr2.length];
	    sortUp(arr2,temp2);
	    for(int n:arr2){
	    	System.out.print(n+" ");
	    }
	}

}

总结

稳定。
非原地排序。
时间复杂度为NlogN
空间复杂度为N
归并排序的主要缺点是辅助数组所使用的额外空间和N的大小成正比
归并排序的递归使小规模问题中方法的调用过于频繁。使用插入排序处理小规模的子数组（比如长度小于15）一般可以将归并排序的运行时间缩短10%-15%
当数组长度为2的幂时，自顶向下和自底向上的归并排序所用的比较次数和数组的访问次数正好相同，只是顺序不同。其它时候，两种方法的比较和数组的访问次序会有所不同

GitHub：https://github.com/AlbertKnag/algs-practice

上一篇：排序算法04：希尔排序
下一篇：排序算法06：快速排序