排序算法08：优先队列与堆排序

2017-05-01

堆排序一种是基于二叉堆的排序。本文将从优先队列讲起，循序渐进的实现堆排序。这也是《算法》第四版上讲解堆排序的大致章节结构。另外，本文所有的图都来自于此书。

优先队列

普通队列是一种先进先出的数据结构，先放进队列的元素取值时优先被取出来。而优先队列是一种具有最高优先级元素先出的数据结构，比如每次取值都取最大的元素。

优先队列有两个核心方法，一个是insert(val)向队列中添加元素，另外一个是delMax()删除最大元素（优先级最高的）并返回。可以考虑使用数组来存储优先队列的数据。

优先队列有如下三种实现方式：

有序数组(调用insert方法时使用类似插入排序把新增元素放到正确位置，调用delMax方法时直接取数组最后一个元素，因为此时元素已经是有序状态)
无序数组（调用insert方法时直接把元素放到数组中，调用dexMax方法时使用类似选择排序的方法从数组中找出最大元素，删除并返回）
堆

堆的算法

优先队列可以使用一棵堆有序的二叉树来解决。什么叫做堆有序呢？当一棵二叉树的每个几点都大于它的两个子节点时，它被称为堆有序。那么，根节点就是堆有序的二叉树中的最大节点。

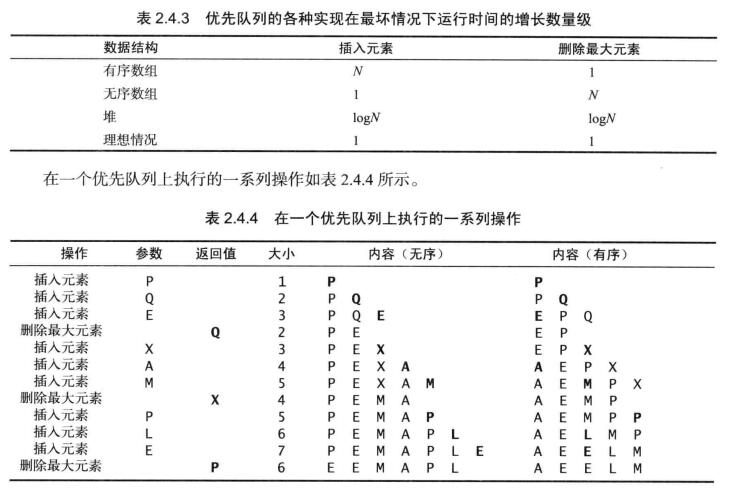
二叉堆可以使用数组来存储。为了方便起见，根节点放在位置1处（位置0不使用），它的两个子节点分别放在位置2和位置3。同理可知，在一个堆中，位置k的节点的父节点的位置为k/2，而它的两个子节点的位置则分别为2k和2k+1.我们就可以这样在树的上下移动：访问a[k]节点的上一层就令k等于k/2，向下一层就令k等于2k或2k+1.

如下图所示：

使用二叉堆，我们就能实现对数级别的插入元素和删除最大元素。

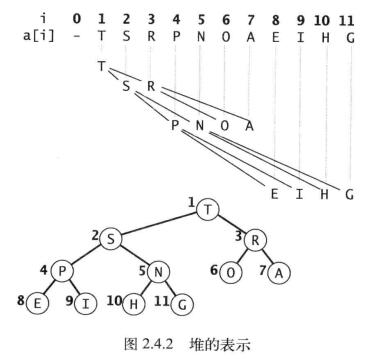
由下自上的堆有序化（上浮）

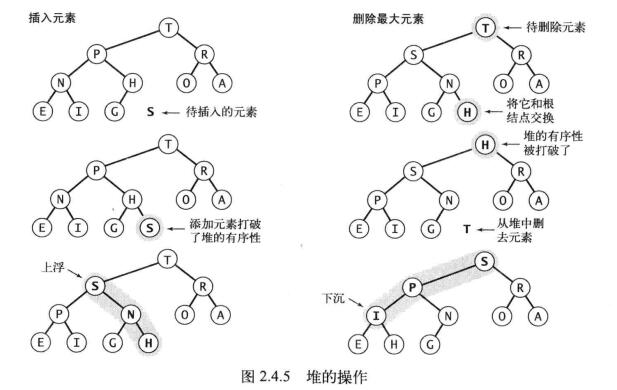
当调用优先队列的insert方法时，我们首先把元素放置到数组的结尾，然后再把该元素上浮到正确的节点，最终形成堆有序状态。

代码如下：

//下标为k的元素上浮到正确位置
function swim(arr,k) {
    while(k>1 && less(arr,parseInt(k/2),k)){
        //父节点索引
        var parentNode = parseInt(k/2);
        exch(arr,parentNode,k);
        k = parentNode;
    }
}

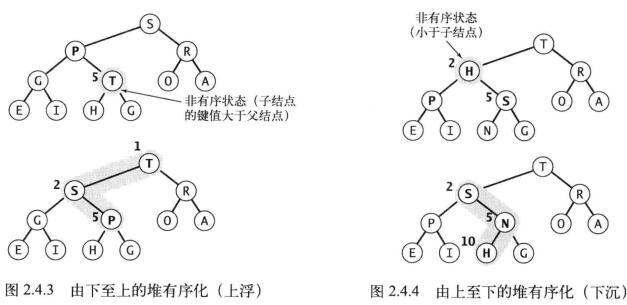
由上至下的堆有序化（下沉）

当调用优先队列的delMax方法时，我们下标为1的元素（最大元素）和数组最后一个元素交换，返回最大元素，数组长度减去1，即删除最后一个元素。此时的位置1元素不一定是最大元素，就需要下沉到正确位置，重新构造有序堆。

代码如下：

//下标为k的元素下沉到正确位置
function sink(arr,k,len) {
    var len = len ||arr.length;
    while(2*k <= len){
        var j = 2*k;
        if(j<len && less(arr,j,j+1)) j++;
        if(!less(arr,k,j)) break;
        exch(arr,k,j);
        k = j;
    }
}

堆有序化示例图：

堆的操作示例图：

优先队列实现

理解了实现堆有序的上浮和下沉两种方法，优先队列的实现就轻而易举了，代码如下：

/**
 * 优先队列
 * @constructor
 */
function MaxQueue() {
    this.queue = [];                //- 存储基于堆的完全二叉树
    this.len   = 0;                 //- 存储于queue[1..len]中，queue[0]未使用
}

/**
 * 向优先队列中插入元素
 * @param val
 */
MaxQueue.prototype.insert = function (val) {
    this.queue[++this.len] = val;    //- 从索引1开始添加元素
    //使新增元素上浮到树的正确位置
    swim(this.queue,this.len);
};

/**
 * 删除优先队列中的最大元素，并返回该元素
 * @returns {*}
 */
MaxQueue.prototype.delMax = function () {
    var max = this.queue[1];        //- 从根节点得到最大元素
    exch(this.queue,1,this.len--);  //- 把最后一个节点放到根节点上，并且让长度索引减一
    this.queue.length = this.len+1; //- 删除最后一个节点
    sink(this.queue,1);             //- 下沉根节点，恢复堆的有序性
    return max;
};

MaxQueue.prototype.show = function () {
    console.log(this.queue);
};

MaxQueue.prototype.isEmpty = function () {
    return this.len==0;
};

示例图：

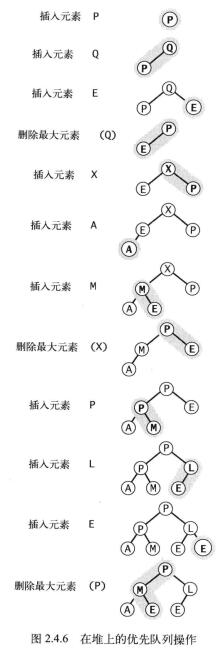
堆排序

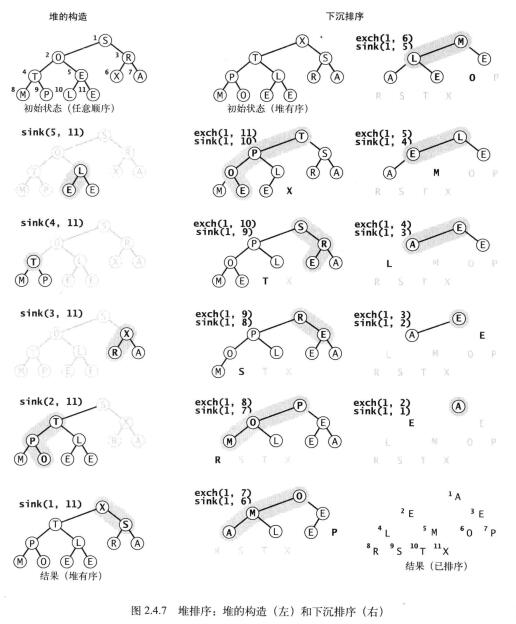
理解了优先队列，堆排序的逻辑十分简单。第一步：让数组形成堆有序状态；第二步：把堆顶的元素放到数组最末尾，末尾的放到堆顶，在剩下的元素中下沉到正确位置，重复操作即可。

代码如下：

/**
 * 堆排序算法
 * @constructor
 */
function HeapSort() {}
HeapSort.prototype.sort = function (arr) {
    var len = arr.length;
    //由于arr[0]不使用，放到最后使得能够被排序
    //注意：也可在less和exch中解决，见后面的Java完整代码实现。这里为了对应位置1的元素不使用，方便对照看代码与样例图。
    arr[len] = arr[0];
    //使用下沉来构造二叉堆
    for(var k=parseInt(len/2);k>=1;k--){
        sink(arr,k,len);
    }
    //不断把最大的arr[1]交换到最后，然后让新的arr[1]元素下沉到堆有序状态
    while (len>1){
        exch(arr,1,len--);
        sink(arr,1,len);
    }
    //删除未使用的arr[0]（也可在less和exch中解决，见Java代码实现）
    arr.splice(0,1);
};

示例图：

完整代码

Javascript实现

/**
 * Created by YiYing on 2017/5/2.
 */
(function (W) {

    /**
     * 优先队列
     * @constructor
     */
    function MaxQueue() {
        this.queue = [];                //- 存储基于堆的完全二叉树
        this.len   = 0;                 //- 存储于queue[1..len]中，queue[0]未使用
    }

    /**
     * 向优先队列中插入元素
     * @param val
     */
    MaxQueue.prototype.insert = function (val) {
        this.queue[++this.len] = val;    //- 从索引1开始添加元素
        //使新增元素上浮到树的正确位置
        swim(this.queue,this.len);
    };

    /**
     * 删除优先队列中的最大元素，并返回该元素
     * @returns {*}
     */
    MaxQueue.prototype.delMax = function () {
        var max = this.queue[1];        //- 从根节点得到最大元素
        exch(this.queue,1,this.len--);  //- 把最后一个节点放到根节点上，并且让长度索引减一
        this.queue.length = this.len+1; //- 删除最后一个节点
        sink(this.queue,1);             //- 下沉根节点，恢复堆的有序性
        return max;
    };

    MaxQueue.prototype.show = function () {
        console.log(this.queue);
    };

    MaxQueue.prototype.isEmpty = function () {
        return this.len==0;
    };

    W.MaxQueue = MaxQueue;


    /**
     * 堆排序算法
     * @constructor
     */
    function HeapSort() {}
    HeapSort.prototype.sort = function (arr) {
        var len = arr.length;
        //由于arr[0]不使用，放到最后使得能够被排序
        //注意：也可在less和exch中解决，见后面的Java完整代码实现。这里为了对应位置1的元素不使用，方便对照看代码与样例图。
        arr[len] = arr[0];
        //使用下沉来构造二叉堆
        for(var k=parseInt(len/2);k>=1;k--){
            sink(arr,k,len);
        }
        //不断把最大的arr[1]交换到最后，然后让新的arr[1]元素下沉到堆有序状态
        while (len>1){
            exch(arr,1,len--);
            sink(arr,1,len);
        }
        //删除未使用的arr[0]（也可在less和exch中解决，见Java代码实现）
        arr.splice(0,1);
    };

    W.HeapSort = HeapSort;


    //下标为k的元素上浮到正确位置
    function swim(arr,k) {
        while(k>1 && less(arr,parseInt(k/2),k)){
            //父节点索引
            var parentNode = parseInt(k/2);
            exch(arr,parentNode,k);
            k = parentNode;
        }
    }

    //下标为k的元素下沉到正确位置
    function sink(arr,k,len) {
        var len = len ||arr.length;
        while(2*k <= len){
            var j = 2*k;
            if(j<len && less(arr,j,j+1)) j++;
            if(!less(arr,k,j)) break;
            exch(arr,k,j);
            k = j;
        }
    }

    function less(arr,m,n) {
        //可根据不同的数据类型设置比对规则，比如json。这里适用于数字与字符串。
        return arr[m]<arr[n];
    }

    /**
     * 交换数组arr中m与n的位置
     * @param m
     * @param n
     */
    function exch(arr,m,n) {
        var swap    = arr[m];
        arr[m]      = arr[n];
        arr[n]      = swap;
    }


})(window);

//测试代码
(function () {
    //优先队列测试，依次从大到小输出元素
    var q = new MaxQueue();
    q.insert(3);
    q.insert(33);
    q.insert(9);
    q.insert(21);
    while (!q.isEmpty()){
        console.log(q.delMax())
    }

    //堆排序测试代码
    var arr = [4,5,6,0,3,5,21,7,9,0,1];
    new HeapSort().sort(arr);
    console.log(arr);
})();

Java实现

package com.algs;

public class Heap {
	/**
	 * 堆排序
	 * @param pq
	 */
	public static void sort(Comparable[] pq) {
        int n = pq.length;
        //构造堆结构
        for (int k = n/2; k >= 1; k--)
            sink(pq, k, n);
        //排序数组
        while (n > 1) {
            exch(pq, 1, n--);
            sink(pq, 1, n);
        }
    }

	//下沉元素
	private static void sink(Comparable[] pq, int k, int n) {
        while (2*k <= n) {
            int j = 2*k;
            if (j < n && less(pq, j, j+1)) j++;
            if (!less(pq, k, j)) break;
            exch(pq, k, j);
            k = j;
        }
    }

	//注意这里i和j都减去1
    private static boolean less(Comparable[] pq, int i, int j) {
        return pq[i-1].compareTo(pq[j-1]) < 0;
    }
    //注意这里i和j都减去1
    private static void exch(Object[] pq, int i, int j) {
        Object swap = pq[i-1];
        pq[i-1] = pq[j-1];
        pq[j-1] = swap;
    }

    private static void show(Comparable[] a) {
        for (int i = 0; i < a.length; i++) {
            System.out.println(a[i]);
        }
    }

	public static void main(String[] args) {
		String[] a = {"S","O","R","T","E","X","A","M","P","L","E"};
        Heap.sort(a);
        show(a);
	}
}

总结

不稳定。
原地排序。
时间复杂度为NlogN
空间复杂度为l

GitHub：https://github.com/AlbertKnag/algs-practice

上一篇：排序算法07：三向快速排序
下一篇：排序算法09：总结